LeetCode六月挑战（6.14） Cheapest Flights Within K Stops LeetCode787解题报告

不知不觉半个月过去了，六月还有半个月哦，加油！

题目

There are n cities connected by m flights. Each flight starts from city u and arrives at v with a price w.

Now given all the cities and flights, together with starting city src and the destination dst, your task is to find the cheapest price from src to dst with up to k stops. If there is no such route, output -1.

Example 1:
Input:
n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]
src = 0, dst = 2, k = 1
Output: 200
Explanation:
The graph looks like this: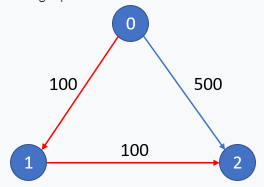

The cheapest price from city 0 to city 2 with at most 1 stop costs 200, as marked red in the picture.
Example 2:
Input:
n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]
src = 0, dst = 2, k = 0
Output: 500
Explanation:
The graph looks like this:
The cheapest price from city 0 to city 2 with at most 0 stop costs 500, as marked blue in the picture.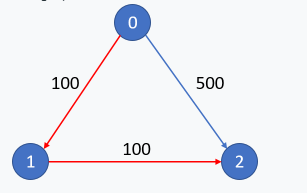

思路

思路主要由三种：BFS，DFS，DP。BFS和DFS在做的过程中都需要做剪枝处理。Jungle这里采用了DP的方法，DP的方法的核心思想是Bellman-Ford 算法。当不可以转机时，到达目的地1和目的地2的花费分别为100和500，当最多可以转一次机时，直达是500，先转机到1再到2的花费为200。所以最少花费为200.由此得到DP公式dp[i][v] = min(dp[i][v], dp[i-1][u] + cost[u][v]) ，比较直接从i起始地到v目的地的花费和从上一站i-1起始站中转到达v目的地的花费，取两者间的较小的值作为该目的地的最小花费，以便后续作为起始站进行后续的计算。具体代码我们简化DP为一维数组，另设一个cost花费数组记录结果。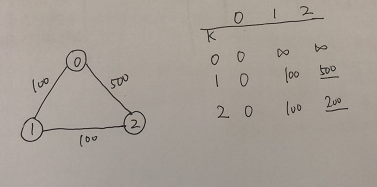

代码

class Solution {
    public int findCheapestPrice(int n, int[][] flights, int src, int dst, int K) {
        int max_Cost = 1<<30;
        int[] cost = new int[n];
        Arrays.fill(cost,max_Cost);
        cost[src] =0;
        for(int i=0;i<K+1;i++){
            int[] tran = cost.clone();
            for(int[] flight: flights)
                tran[flight[1]] = Math.min(tran[flight[1]], cost[flight[0]]+flight[2]);
            cost = tran;
        }
        return cost[dst]>= max_Cost ? -1 : cost[dst];
    }
}